 |
 |
 |
|
| Stahldraht | Laschpunkt | Stahlband |
 |
 |
|
| Kontrollieren und Messen von Lascheinrichtungen | ||
Bemerkung: Kursiv gedruckte Teile sind mit freundlicher Genehmigung von Herrn Kapitän Professor Hermann Kaps einer seiner Seminarzusammenstellungen entnommen.
Grundbegriffe
Kilonewton (kN) ist eine handliche Einheit für die Kraft, um z. B. die Bruchkraft oder Bruchfestigkeit von Ladungssicherungsmaterial zu beschreiben. Es ersetzt die früher übliche metrische Tonne, die nach SI-Norm für die Beschreibung der Masse vorgesehen ist. Zur Umgewöhnung kann man sich merken: 1 kN ≡ 0,1 t oder 100 kg.
Diejenigen, die früher gern in der Masseeinheit Kilogramm gerechnet haben, können die Einheit Dekanewton (daN) als Krafteinheit benutzen.
Im Folgenden werden einige Begriffe in englischer Sprache erklärt, die in der Schifffahrt zunehmend in Gebrauch sind.
Securing element ist ein einzelnes Stück aus der Ausrüstung eines Schiffes zur Ladungssicherung, wie z. B. ein Schäkel, ein Decksring, eine Spannschraube, Kette oder Drahtseil.
Securing device ist eine geeignete Kombination von Elementen, die ein eigenständiges Ladungssicherungsmittel ergeben, z. B. einen Lasching oder eine Pallung.
Securing Arrangement ist eine sinnvolle Anordnung von Ladungssicherungsmitteln, die dazu gedacht ist, ein Ladungsstück oder einen Ladungsblock zu sichern.
Breaking Load (BL) ist die nominelle Bruchlast, die in der Regel vom Hersteller angegeben werden sollte. Sie kann jedoch andernfalls durch Faustformeln abgeschätzt werden.
Maximum Securing Load (MSL) in kN ist die größte akzeptable Kraft, die einem Ladungssicherungselement oder -mittel zugemutet werden kann. Im Deutschen ist der Begriff Einsatzfestigkeit geeignet.
Calculation Strength (CS) in kN ist eine Rechenkraft, zu deren Ermittlung MSL verkleinert wird nach der Formel: CS = MSL / 1.5. CS-Werte werden ausschließlich in der Bilanzrechnung nach Annex 13 des CSS-Codes verwendet.
Der Zusammenhang zwischen Breaking Load und Maximum Securing Load wird im Annex 13 durch folgende Tabelle dargestellt:
| Material | MSL |
| shackles, rings, deck eyes, turnbuckles of mild steel |
50 % of breaking strength |
| fibre ropes | 33 % of breaking strength |
| web lashing | 70 % of breaking strength |
| wire rope (single use) | 80 % of breaking strength |
| wire rope (re-useable) | 30 % of breaking strength |
| steel band (single use) | 70 % of breaking strength |
| chains | 50 % of breaking strength |
| timber | 0,3 kN per cm² normal to the grain |
Tabelle: Bestimmung von MSL aus der Bruchlast
Zurrelemente und Zurrmittel. Es gibt keine internationalen Normen für Zurrelemente und Zurrmittel. Man kann allenfalls erwarten, dass der Hersteller oder Händler beim Kauf die nominelle Bruchlast mitteilt oder bescheinigt. Dabei ist meist unklar, wie dieser Wert ermittelt wurde und unter welchen Bedingungen er gilt. Andere Angaben, wie Elastizität und Dauerfestigkeit, werden nicht genannt.
Nachstehend werden tabellarisch die wichtigsten Materialien und Elemente mit den üblichen Kennwerten aufgelistet. Unter Bruchlast wird eine anerkannte Faustregel wiedergegeben.
Werden für die Abmessungen Millimeter statt Zentimeter gewählt, ergeben sich anstelle von Kilonewton-Werten für die Bruchlast solche in Dekanewton [daN].
| Material / Element | Bruchlast [kN] | Hinweise |
| Naturfasertauwerk (Manila, Sisal, Hanf) | 6 · d² | d = Seildurchmesser in cm. Naturfaserseile sind empfindlich gegen Verrottung und gegen Säuren und Laugen. Alle Faserseile sind empfindlich gegen Scheuern an scharfen Kanten. Knoten von Kunstfaserseilen können aufrutschen. Zum Spannen sollten Drehknüppel ausreichender Stärke verwendet und diese gegen Aufdrehen gesichert werden. |
| Polypropylen | 12 · d² | |
| Polyester | 15 · d² | |
| Polyamid | 20 · d² | |
| Herkules (Sisal) | 6 · d² | |
| Herkules (Polypropylen) | 12 · d² |
| Material / Element | Bruchlast [kN] | Hinweise |
| Drahtseil 6 · 9 + 1 FC Drahtseil 6 · 19 + 1 FC Drahtseil 6 · 37 + 1 FC |
50 · d² | d = Seildurchmesser in cm. Die Herstellung von konventionellen Drahtseillaschingen mit Spannschrauben und Seilklemmen ist handwerklich anspruchsvoll und birgt eine Fülle von Fehlerquellen. Im Anschluss an diese Tabelle werden ausführliche Hinweise gegeben. |
| Drahtseil 6 · 9 + 7 FC Drahtseil 6 · 12 + 7 FC Drahtseil 6 · 15 + 7 FC |
25 · d² |
| Material / Element | Bruchlast [kN] | Hinweise |
| Schäkel | 20 · d² | d = Bolzendurchmesser in cm. Die Bruchlastformel gilt nur für Schäkel aus normalfestem Stahl. |
| Spannschrauben | 20 · d² | d = Gewindedurchmesser in cm. Die Bruchlastformel gilt nur für Spannschrauben aus normalfestem Stahl. |
| Material / Element | Bruchlast [kN] | Hinweise |
| Stahlband unbehandelt Stahlband gebläut |
70 · b · d 85 · b · d |
b = Bandbreite in cm d = Banddicke in cm. |
| Material / Element | Bruchlast [kN] | Hinweise |
| Ketten, lang- und kurzgliedrig mit unterschiedlichen Spannelementen | siehe Herstellerangabe | Zurrketten werden zur Gewichtseinsparung stets aus höherfestem Stahl hergestellt. Deshalb ist man hinsichtlich der Bruchlast auf die Herstellerangaben angewiesen. |
| Material / Element | Bruchlast [kN] | Hinweise |
| Decksringe und Augplatten | 20 · d² | d = Durchmesser des Ringmaterials in cm. Die Bruchlastformel gilt nur für Material aus normalfestem Stahl. |
| Material / Element | Bruchlast [kN] | Hinweise |
| Zurrgurte aus Kunstfasern | siehe Herstellerangabe | Zurrgurte werden in unterschiedlichen Qualitäten hergestellt. Sie sind hoch elastisch, zeigen aber bei Schwellbelastungen über 50 % der Bruchlast bleibende Verformung und werden daher schnell lose. Sie dürfen nicht geknotet werden. In ihren Empfindlichkeiten gleichen sie den Kunstfaserseilen. |
| Material / Element | Bruchlast [kN] | Hinweise |
| Schweißverbindungen, die auf Scherung beansprucht werden | MSL = 4 kN pro cm | Einlagige Schweißung von 4 mm Dicke. |
| MSL = 10 kN pro cm | Dreilagige Schweißung von 10 mm Dicke. |
| Material / Element | Bruchlast [kN] | Hinweise |
| Nadelholz zur Pallung | MSL = 0,3 kN pro cm² | Druckbelastung quer zur Faser |
| Nadelholz zur Pallung | MSL = 1 kN pro cm² | Druckbelastung längs zur Faser |
| Material / Element | Bruchlast [kN] | Hinweise |
| Spezielle Ausrüstung für Ro-ro-Schiffe | - | Trailer Horses, Trailer Jacks, Radkeile; Bruchlasten üblicherweise unbekannt |
| Spezielle Ausrüstung für Containerschiffe | siehe Herstellerangabe | Laschstangen, Spannschrauben, Twistlocks, D-Ringe, Sockel für Einschübe, Brückenfittinge, Verbindungsplatten usw. Festigkeit und Materialeigenschaften nach den Forderungen der jeweiligen Klassifikationsgesellschaft |
Aus wirtschaftlicher Sicht ist es erstrebenswert, Ladungssicherungsmittel und Ladungssicherungsanordnungen homogen zu gestalten.
- Ein homogenes Ladungssicherungsmittel setzt sich aus Elementen zusammen, die soweit wie möglich gleiche MSL-Werte besitzen.
- Eine homogene Ladungssicherungsanordnung besteht aus Ladungssicherungsmitteln, die so angeordnet sind, dass sie unter äußerer Belastung den ihrer Stärke entsprechenden Teil der Last tragen.
Beispiel Niederzurrung:
 |
 |
|
| Gebrauch von Niederzurrungen | ||
Die Holzkiste auf dem Flat habe eine angenommene Gewichtskraft von 12.000 daN. Ohne die Kippgefahr bei dieser überhohen Kiste zu berücksichtigen, soll das Packstück für den Überseeversand gesichert werden. Danach wäre von 0,8 g seitlichen Beschleunigungen auszugehen. Es ist demnach mit seitlichen Kräften in Höhe von 12.000 daN · 0,8 zu rechnen bzw. mit 120 kN · 0,8. Das sind 9.600 daN bzw. 96 kN.
Die auf der linken Abbildung benutzten Einweg-Textilgurte haben eine Bruchlast von 3.433 daN. Bei einem MSL von maximal 70 % der Bruchlast wären das 2.403 daN. Davon dürften maximal die Hälfte, also ca. 1.200 daN als Vorspannung eingebracht werden. Es sei angemerkt, dass dieser Wert in der Praxis weder erreicht noch während der ganzen Reise gehalten werden kann.
Die wirksame Länge des Gurtes (rote Linie) von der Befestigung am Laschpunkt bis zur Kistenkante wird mit 3,00 m gemessen. Die wirksame Höhe (grüne Linie) wird mit 2,93 m bestimmt - einem sehr hohen Vertikalanteil von 97,6 %, der für jede Ladung ermittelt werden kann, indem die wirksame Höhe durch die wirksame Länge dividiert wird. Mit der Vorspannung multipliziert ergibt das die Kraft, mit der die Ladung auf der gespannten Seite auf das Flat gezogen wird. Im Beispiel sind das 97,6 % von 1.200 daN, also 1.171 daN. Unterstellt man den Idealfall, dass sich diese Kraft voll auf die andere Seite überträgt, ist von einer Gesamtvorspannung pro Überwurflasching von 2.342 daN auszugehen. Wird eine Reibung von 30 % unterstellt, kann mit einem Überwurflasching eine Sicherungskraft von ca. 703 daN erreicht werden. Um die Kiste zu sichern, sind theoretisch 13,65 Gurte erforderlich (9.600 daN : 703 daN). In der Wirklichkeit dürfte mit den benutzten Textilgurten höchstens eine Vorspannkraft von ca. 100 daN bis 200 daN während der Reise gehalten werden können. Das heißt, dass mit einem Gurt eine dauerhafte Sicherungskraft von 30-60 daN gehalten werden kann. Um die Kiste wirklich "gesichert zu haben", müssten demnach 320-160 Gurte vorgesehen werden!!!
| Merksatz: Überwurflaschings sichern nur über den Vertikalanteil der Vorspannung in Verbindung mit der Reibung. |
| Merksatz: Die Vorspannung darf nie größer als 50% des MSL des schwächsten "securing element" sein. |
Diese Rechnung nach Backrezept ist einfacher und genauer als eine Bestimmung über den Zurrwinkel α, da sich in der Laschpraxis Strecken besser messen lassen als Winkel. Soll der Vertikalanteil eines Laschings über den Winkel bestimmt werden, ist die zulässige Zurrkraft mit dem Sinus des Zurrwinkels zu multiplizieren: Vertikalanteil = MSL · sin α.
Je kleiner dabei die Zurrwinkel sind, umso kleiner fällt der Vertikalanteil aus. Bei 90° Zurrwinkel sind es 100 % (sin 90° = 1), bei 75° 97 % (sin 75° = 0,9659), bei 60° 87 % (sin 60° = 0,866), bei 45° 71 % (sin 45° = 0,7071), bei 30° 50 % (sin 30° = 0,5), bei 15° 26 % (sin 15° = 0,2588) und bei 0° Zurrwinkel 0 % (sin 0° = 0).
Beispiel Direktzurrung:
Der wesentliche Unterschied zum Überwurflasching besteht darin, dass bei Direktzurrungen die Vorspannung möglichst klein gehalten werden kann und soll.
| Merksatz: Die Vorspannung sollte bei Direktzurrungen möglichst kleine sein. Es darf aber nie Lose in einen Lasching kommen können. |
Sie muss allerdings so groß sein, dass keine Lose in einen Lasching kommen kann. Die dahinter steckende Erkenntnis ist die, dass unter Beanspruchung der Lasching bis an sein MSL belastet werden darf und dass die dabei entstehenden Vertikalkomponenten zusätzliche Reibungskräfte bewirken.
 |
Direktzurrung mit Ketten |
Mit einem besonderen Hang zur Mathematik können die entsprechenden Zurrkräfte errechnet werden, indem zuerst der Zurrwinkel α mit 47,5° bestimmt wird und dann die vertikalen und horizontalen Anteile über die Sinus- und Cosinus-Funktion des Winkels in Zusammenhang mit der zulässigen Zurrkraft der Kette in Verbindung gebracht werden.
Nach Backrezept geht es auch ohne Winkelbestimmung und Winkelfunktionen. Es reichen die Grundrechenarten aus. Mit einem Bandmaß oder einem Gliedermaßstab (früher: Zollstock) werden folgende Längen bestimmt: die wirksame Länge der Zurrkette (rote Linie mit 3,61 m), die wirksame Vertikalkomponente (grüne Linie mit 2,66 m) und die wirksame Horizontalkomponente (blaue Linie mit 2,44 m). Über die Faustregeln oder die Herstellerangaben werden die Bruchlast und das MSL der hochfesten Kette mit 13 mm Stahldurchmesser bestimmt. Es sind 10.000 daN. Eine Kontrollmessung des Laschpunktes ergibt einen Stahldurchmesser von 28,3 mm. Daraus ergibt sich eine Bruchkraft von 16.000 daN und ein MSL von 8.000 daN. Dieser Wert stellt eine Obergrenze dar, falls die Kettenkomponenten höher ausfallen.
Vertikale Sicherungskraft: 2,66 m : 3,61 m · 10.000 daN = 7.368 daN. Eine Laschkette sichert das Packstück nach oben gegen Wegfliegen mit 7.368 daN. Aber das ist nicht so bedeutsam. Diese Kraft wird bei einer Horizontalbewegung des Packstückes beim Straffen der Kette wirksam, wodurch das Packstück mit diesem Wert auf den Boden gezogen wird. Bei einem angenommenen Gleit-Reibbeiwert von 30 % (μ = 0,3) wird das Packstück durch einen Lasching in allen Richtungen mit einer Kraft von 7.368 daN · 0,3 = 2.210 daN gesichert.
Horizontale Sicherungskraft: 2,44 m : 3,61 m · 10.000 daN = 6.759 daN. Eine Laschkette sichert das Teil direkt mit 6.759 daN in Querrichtung. Dazu kommen die vorher ermittelten zusätzlichen Sicherungskräfte über die Reibung in Höhe von 2.210 daN. Damit sichert der bezeichnete Kettenlasching das Anlageteil in Querrichtung gegen Bewegungen nach rechts mit 8.969 daN.
Da keine Längskomponenten vorhanden sind, sichert eine Kette das Kollo nur mit den über die Vertikalkomponente bewirkten Reibungskräften mit 2.210 daN in Längsrichtung.
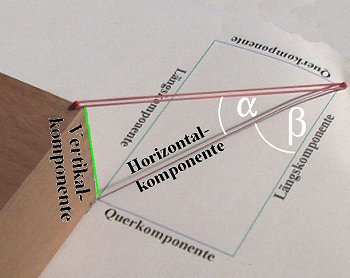 |
unterschiedliche Komponenten bei einem Diagonal- lasching mit Zurrwinkeln |
Sollen die jeweiligen Sicherungskräfte in Längs-, Quer- und Vertikalrichtung über die Zurrwinkel α und β bestimmt werden, ist folgendermaßen zu rechnen:
| Komponente | Rechnung |
| Vertikalkomponente | MSL · sin α |
| Horizontalkomponente | MSL · cos α |
| zusätzliche Reibungskräfte | Vertikalkomponente · μ oder MSL · sin α · μ |
| reine Querkomponente | Horizontalkomponente · sin β oder MSL · cos α · sin β |
| reine Längskomponente | Horizontalkomponente · cos β oder MSL · cos α · cos β |
Da die durch die Vertikalkomponente bewirkten zusätzlichen Reibungskräfte den Kräften durch Quer- und Längskomponente zugerechnet werden dürfen, ergeben sich als Sicherungskräfte:
| Sicherungskräfte | Rechnung |
| Vertikalsicherung | MSL · sin α |
| Quersicherung | MSL · cos α · sin β + MSL · sin α · μ |
| Längssicherung | MSL · cos α · cos β + MSL · sin α · μ |
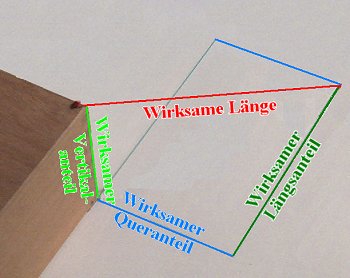 |
Bestimmung der Sicherungskräfte |
Nach Backrezept geht es schneller, einfacher und genauer. Es sind vier Längenmessungen vorzunehmen und das MSL des schwächsten Ladungssicherungselementes ist zu bestimmen. Der Reibungskoeffizient ist zu ermitteln oder zu schätzen.
| Sicherungskräfte | Rechnung |
| Vertikalsicherung | wirksamer Vertikalanteil : wirksame Länge · MSL |
| zusätzliche Reibungskräfte | wirksamer Vertikalanteil : wirksame Länge · MSL · μ |
| Quersicherung incl. zus. Reibungskräfte | wirksamer Queranteil : wirksame Länge · MSL + wirksamer Vertikalanteil : wirksame Länge · MSL · μ |
| Längsicherung incl. zus. Reibungskräfte | wirksamer Längsanteil : wirksame Länge · MSL + wirksamer Vertikalanteil : wirksame Länge · MSL · μ |
Rechenbeispiel:
Gesichert wird mit einem doppelt genommenen Einmal-Textilgurt wie zuvor, bei dem aus Gründen der Vorsicht das MSL nicht mit 70 % der Bruchlast, sondern nur mit 30 % der Bruchlast angenommen wird. Alle notwendigen Daten sind in der Skizze vermerkt.
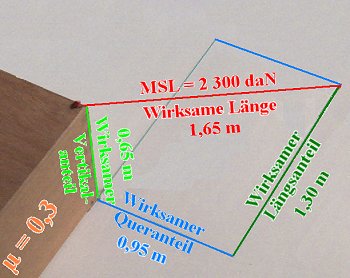 |
Rechenbeispiel: Ermittlung der Sicherungskräfte |
| Sicherungskräfte | Rechnung |
| Vertikalsicherung | 0,65 m : 1,65 m · 2.300 daN = 906 daN |
| zusätzliche Reibungskräfte |
0,65 m : 1,65 m · 2.300 daN = 906 daN · 0,3 = 271,8 daN |
| Quersicherung incl. zus. Reibungskräfte |
0,95 m : 1,65 m · 2.300 daN = 1.324 daN + 271,8 daN = 1.595,8 daN |
| Längsicherung incl. zus. Reibungskräfte |
1,30 m : 1,65 m · 2.300 daN = 1.812 daN + 271,8 daN = 2.083,8 daN |
Für die Gesamtsicherung muss immer betrachtet werden, unter welchen Umständen welche Laschings beansprucht werden:
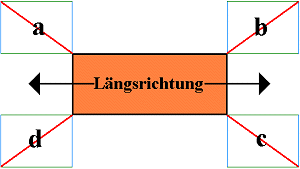 |
mit vier diagonalen Direktzurrungen gesichertes Kollo |
| nach oben | 4 x Vertikalsicherung = 4 x 906 daN | 3.624 daN |
| längs nach links | Es halten b und c je mit ihrem Längsanteil | 4.167,6 daN |
| längs nach rechts | Es halten a und d je mit ihrem Längsanteil | 4.167,6 daN |
| quer nach oben | Es halten d und c je mit ihrem Queranteil | 3.191,6 daN |
| quer nach unten | Es halten a und b je mit ihrem Queranteil | 3.191,6 daN |
Als Feststellung bleibt, dass die Laschanordnung inhomogen ist, wenn die Musterladung auf einem Flat geladen wäre, dass im Längsstau auf einem Containerschiff befördert wird, bei dem angenommen wird, dass in Längsrichtung Beschleunigungen von 0,4 g und in Querrichtung solche von 0,8 g wirken. Unter dieser Voraussetzung hätten die Laschings so angebracht werden müssen, dass die Querkomponente doppelt so groß wie die Längskomponente ist:
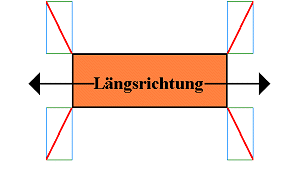 |
Querkomponenten doppelt so groß wie die Längs- komponenten |
Wird davon ausgegangen, dass das Flat im Längsstau auf einem Containerschiff befördert wird und im Vor- und/oder Nachlauf auf einem Straßenfahrzeug befördert wird, hätten Längs- und Querbeschleunigungen von je 0,8 g als Ausgangswert für die Befestigung der Laschings dienen müssen.
Hier ist die Entscheidung einfach: Beide Komponenten müssen gleich groß sein.
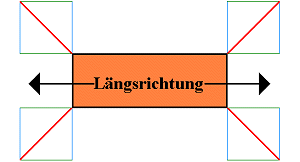 |
Quer- und Längskomponenten gleich groß |
Soll das Flat im Vor- oder Nachlauf auf einem Eisenbahnwaggon im kombinierten Ladungsverkehr befördert werden, ist von 1 g in Längsrichtung auszugehen. Wenn von Querbeschleunigungen von 0,8 g auszugehen ist, müssen die Längskomponenten um 25 % größer als die Querkomponenten sein bzw. die Querkomponenten müssen 20 % kleiner als die Längskomponenten ausfallen:
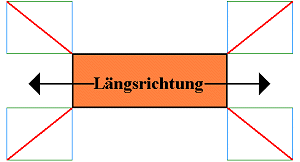 |
Längskomponenten sind um ein ein Viertel größer als die Querkomponenten |
Auch beim Gebrauch von Umspannungen kommt es zu Winkeln, die eine Minderung des MSL bewirken. Die Auswirkungen sind nicht sehr dramatisch, denn sie sind eine Kosinus-Funktion des halben Spreizwinkels zwischen den Parten. Prinzipiell ist es gleichgültig, ob Winkel gemessen und die Kräfte berechnet oder ob Strecken gemessen werden. Für mit der Mathematik vertraute Personen ist es einfacher, mit der Winkelfunktion zu rechnen als zu messen, sofern ein Taschenrechner mit Winkelfunktionen oder eine entsprechende Tabelle zur Verfügung stehen. Beide Methoden sind machbar. Wer den Verlauf einer Kosinuskurve kennt oder einige Werte im Kopf hat, kann auch überschlägig rechnen.
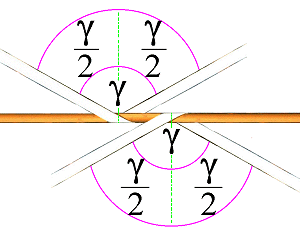 |
nicht mehr zulässiger Winkel |
Der Winkel γ beträgt 121,552°, aber wer kann schon so genau einen Winkel bestimmen. Der halbe Winkel ist demnach 60,776°. Der Kosinus dieses Winkels ist 0,488. Daraus ist ersichtlich, dass diese Form der Sicherung nichts gebracht hat. Denn die rechnerisch bestimmte Part erzeugt nur Sicherungskräfte von weniger als der Hälfte. Da hätte man besser mit einer einsträngigen Direktzurrung sichern können. Der Kosinus von 60° beträgt 0,5. Damit ist klar, dass Umspannungen sich nur lohnen können, wenn die Spreizwinkel - also das volle γ - deutlich kleiner als 120° sind, γ/2 also deutlich kleiner als 60° sein muss. Gleiches hätte sich - möglicherweise schneller - über eine Messung ergeben:
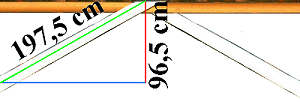 |
wie zuvor: nicht mehr zulässiger Winkel |
Die Messung der wirksamen Länge einer Part der Umspannung beträgt 197,5 cm, die wirksame Querrichtung 96,5 cm. Das ist weniger als die Hälfte. Beide Parten der Umspannung zusammen liegen demnach unter 1. Auch hier wird sofort erkenn- und beweisbar, dass sich diese Umspannung nicht lohnt.
Anders hier:
Hier wird der Spreizwinkel γ mit 27° gemessen (γ/2 beträgt demnach 13,5°). Der Kosinus von 13,5° ist 0,973 - also nahe an 1. Das bedeutet, dass nahezu das Doppelte des MSL durch diese Sicherung erreicht wird, genau sind es das 1,945fache des MSL im Einzelstrang.
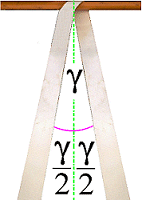 |
praxisnaher Winkel für Umspannungen |
Ungefähr gleiche Ergebnisse hätte eine Messung erbracht:
Wird - nach Backrezept - der kleinere gemessene Wert durch den größeren geteilt, ergibt sich der Wert 0,973. Das heißt, dass eine Umspannung das 2 · 0,973fache, also das 1,946fache des MSL im Einzelstrang hält.
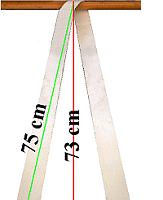 |
wie zuvor: praxisnaher Winkel für Umspannungen |
Korrekterweise muss der Winkel räumlich zwischen den Parten gemessen werden, da Umspannungen, die auf getrennte Laschpunkte gesetzt sind, einen "schrägen" Winkel miteinander bilden. Beim Messen dürften die Probleme nicht auftreten, auch wenn eine Part von oben und die andere von unten kommt.
Hier die groben Richtwerte für das MSL bei geschätzten Winkeln:
| geschätzter Winkel | MSL der Umspannung |
| 120° | 2 x MSL im Einzelstrang · 0,50 = 1,0 · MSL im Einzelstrang |
| 90° | 2 x MSL im Einzelstrang · 0,70 = 1,4 · MSL im Einzelstrang |
| 60° | 2 x MSL im Einzelstrang · 0,87 = 1,7 · MSL im Einzelstrang |
| 40° | 2 x MSL im Einzelstrang · 0,92 = 1,8 · MSL im Einzelstrang |
| 30° | 2 x MSL im Einzelstrang · 0,97 = 1,9 · MSL im Einzelstrang |
| < 30° | 2 x MSL im Einzelstrang · 1,00 = 2,0 · MSL im Einzelstrang |