Das Diagramm in Bild 13 liefert mit dem Eingang "relative Coil-Masse mC/P" die notwendige Länge t der Bettungsträger, abhängig von deren Spreizung s (Kurvenschar links). Dabei ist für Coils von weniger als 0.5 P allein die Spreizung der Bettungsträger von Bedeutung.
Für schwerere Coils, von denen nur jeweils eines geladen werden kann, liefert der Eingang mit der relativen Coil-Masse zunächst die Mindestlänge t der Bettungsträger, die für die Sicherung der Längsfestigkeit erforderlich ist (Begrenzungskurve rechts). Nur wenn die Spreizungen s so klein ist, dass sie längere Balken fordert, gilt natürlich dieser größere Wert (Kurvenschar oberhalb der Begrenzungskurve).
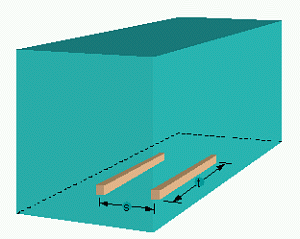
Bild 12: Spreizung s und Länge t von Bettungshölzern oder -trägern
Beispiel 1: mC = 6 t; P = 28 t; mC/P = 0.214; Spreizung der Längshölzer s = 1.0 m: Notwendige Länge t der Längshölzer pro Coil = 1.45 m.
Beispiel 2: mC = 9 t; P = 26 t; mC/P = 0.346; Spreizung der Längshölzer s = 1.2 m: Notwendige Länge t der Längshölzer pro Coil = 1.96 m.
Beispiel 3: mC = 17 t; P = 28 t; mC/P = 0.607; s = 1.4 m: Notwendige Länge t der Längshölzer = 2.80 m. Für die Längsfestigkeit hätte eine Länge t = 2.06 m ausgereicht (blaue Kurve).
Beispiel 4: mC = 20 t; P = 27 t; mC/P = 0.741; s = 1.8 m: Notwendige Länge t der Längshölzer = 3.81 m. Für die Querfestigkeit hätte bei s = 1.8 m eine Länge t von knapp 1.9 m gereicht.
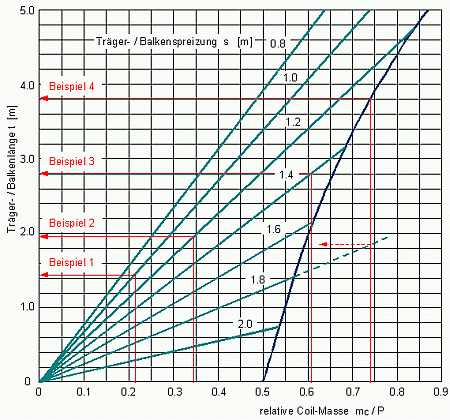
Bild 13: Diagramm zur Bestimmung der notwendigen Bettungsmaße