- Fiber ropes
- Wire ropes and
- Composite or mixed ropes
- Natural fiber ropes and
- Synthetic or man-made fiber ropes
 |
 |
|
| Natural fiber rope | Split fiber rope made of polypropylene |
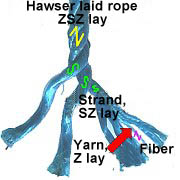
Ropes are made in a number of different ways. Generally, a distinction is made between laid rope and braided rope. In many cases, the way a rope is manufactured determines how it is treated and used. The basic process used to manufacture laid fiber ropes is as follows: When they have been obtained from the raw materials, the fibers are combed to separate them. These are then twisted to produce yarns. In the trade, this is known as laying. If the direction of lay is to the right, it is known as Z-laid, or if it is to the left, it is known as S-laid. In the next stages of the process, the directions of lay are alternated. This is referred to as a 'cross lay' or 'conventional lay'. A cable lay is only used for very strong fiber ropes - but this is not relevant for load securing purposes: In the normal direction of lay, three Z-laid ropes are laid to the left to produce a cable; in the opposite direction of lay, three S-laid ropes are laid to the right to produce the finished cable. The normal direction of lay is also known as Z-lay or ZSZS-lay in and the opposite direction of lay is known as S-lay or SZSZ-lay.
 |
Natural and synthetic fiber ropes - all hawser-laid and Z-laid |
Laid (twisted) ropes are generally used for load securing purposes.
They are generally type A hawser-laid, i.e. a 3-strand rope is used. There are both Z-laid and S-laid versions of this type. The normal direction of lay, however, is to the right.
Natural fiber ropes are no longer used for load securing in most industrialized countries. In some countries, however, natural fiber ropes may be used for securing loads in or on specific cargo transport units. This includes in particular ropes of the following materials:
- Hemp (Ha)
- Manila (Ma)
- Sisal (Si)
- Manila mixed (Ma/Si)
- The ropes become shorter when wet;
- The ropes become longer when dry.
The main raw materials for synthetic fiber ropes are:
- Polyester (PES)
- Polyamide (PA)
- Polypropylene (PP)
- Polyethylene (PE)
- Hempex
Polyamide (generally known under its trade names nylon, perlon etc.) exhibits good behavior with alkalis and solvents but is sensitive to acids. It loses around 20% of its strength per year from natural weathering, especially UV radiation. Because of its price, polyamide is rarely used for load securing purposes.
Polyethylene has no place in load securing on account of its poor mechanical properties. It is even banned for use as slinging ropes.
Hempex is a modified polypropylene material which looks so similar to the natural fiber hemp that it is often confused with it. It is UV-resistant but in terms of its strength not much better than natural fiber ropes. As it is particularly soft, it is sometimes used to fasten tarpaulins etc.
Polypropylene exhibits very good resistance against acids, alkalis and solvents. If it is not stabilized, however, it is very sensitive to natural weathering. For this reason, polypropylene ropes should always be light and heat stabilized. Black dyed ropes are best suited for this. Their strength only decreases at around 5% per year from natural weathering.
There are two main groups of polypropylene ropes:
- monofilament ropes and
- multifilament fiber ropes.
Multifilament ropes exhibit very negative properties when they are dynamically stressed. Movement causes the fibers to separate further, which quickly produces a rupture. This type of stress rarely occurs with load securing. For this reason, composite ropes are produced for load securing purposes generally use multifilament materials.
 |
 |
|
| Steel-reinforced "Hercules" lashing rope | ||
The type of composite rope generally used for lashing purposes is known as "Hercules". This is a rope made of steel wire and natural or synthetic yarns.
Predominantly, "Hercules" made of interwoven polypropylene and wires is sold as lashing material. Ropes of interwoven wire and sisal are no longer commonly used in most industrial countries. "Hercules" has the same strength for lashing purposes as ropes made of sisal or polypropylene with the same diameter, because the wire in Hercules does not have a load-bearing function. The individual wrapped wires have a very low strength and are only intended to increase the rigidity of the material and improve its twisting properties, e.g. when tightening it with a Spanish windlass. The main advantage of "Hercules" over fiber ropes is not its strength but improved handling. In terms of its pure material properties, the same applies as for sisal or polypropylene. It must be stressed again that it exhibits good properties in terms of resistance to aggressive substances.
 |
 |
|
| Thin ropes for securing tarpaulins |
Car secured with "Hercules" lashing |
Fiber ropes are suitable for securing tarpaulins and relatively light loads, e.g.
- Automobiles in or on containers
- Drum cargoes, fiber drums and similar loads in small batches and light receptacles
- Fairly light cases, small batches of boxed goods, individual pallets etc.
 |
 |
|
| 5 mm thick polypropylene rope for securing tarpaulins etc. |
The MSL (Maximum Securing Load) of fiber ropes is 33% of the breaking load. Since the breaking load of polypropylene can be calculated with a rule of thumb using the formula 12 x d², the MSL for the rope shown is 1 kN or 100 daN, depending whether the diameter was specified in centimeters or millimeters.
 |
Calculating the diameter of a polypropylene strap: 5 mm |
| Breaking load | MSL factor | MSL | |
| 0.5 x 0.5 x 12 = 3 kN | x 0.33 = | 1 kN | (diameter in cm) |
| 5 x 5 x 12 = 300 daN | x 0.33 = | 100 daN | (diameter in mm) |
Since a factor of 33% is corresponds to virtually one third, the MSL can also be calculated directly with an easily remembered formula:
| MSL of polypropylene ropes = d x d x 4 |
If a strap or rope is doubled, the values can also be doubled; if it is used four-fold, the values can be quadrupled. It is not possible to increase the values any further, since there is no guarantee that all the runs of rope would be evenly loaded.
 |
Determining the diameter of polypropylene-covered "Hercules": 12 mm |
| Breaking load | MSL factor | MSL | |
| 1.2 x 1.2 x 12 = 17.28 kN | x 0.33 = | 5.76 kN | (diameter in cm) |
| 12 x 12 x 12 = 1,728 daN | x 0.33 = | 576 daN | (diameter in mm) |
It would be rather quicker to calculate this using the direct rule of thumb for the MSL:
| MSL PP "Hercules" 1.2 cm thick = 1.2 x 1.2 x 4 = 5.76 kN |
| MSL PP "Hercules" 12 mm thick = 12 x 12 x 4 = 576 daN |
In this case as well, the values can be doubled or quadrupled respectively for double or (at the most) four-fold use.
| Safety note: Fiber ropes must never be tightened over sharp edges! |
 |
To fabricate a direct lashing with a "Hercules" rope of this type, the necessary rope length is estimated and cut off. The end is threaded through one of the lashing points (A). A loop (B) is knotted into one of the ends using a bowline. The other end is threaded through the second lashing point at (C). The loose end is threaded through the loop of the bowline at (D) and pretensioned by hand. The end is knotted at (E) with at least two half hitches. If greater pretensioning forces are required than those which can be achieved manually, this can be achieved using a Spanish windlass - i.e. using heavers.
If a strap or rope is doubled, the values can also be doubled; if it is used four-fold, the values can be quadrupled. It is not possible to increase the values any further, since there is no guarantee that all the runs of rope would be evenly loaded.
 |
|
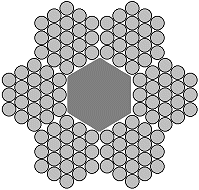
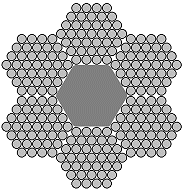
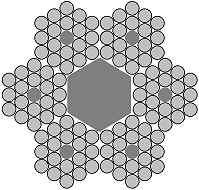
| Different rope structures - cross-sections and plan views |
The type of steel wire ropes mainly used for lashing are cross-laid stranded ropes laid to the right. Occasionally, left-handed cross-lay used.
 |
 |
|
| 6 x 19 + 1 FC | 6 x 37 + 1 FC |
Stranded rope is the designation for a wire rope construction where the individual wires are laid into strands and these are in turn laid into the finished product. The number of individual wires and strands significantly influences the pliability of the wire and its price. The more individual wires there are in a wire rope, the more flexible but also the more expensive it is. A frequently used construction consists of 6 strands each with 19 individual wires per strand, with a fiber core to fill the cavity remaining in the center. The fill factor for rope constructions of this kind is around 0.455, i.e. the cross-sectional area occupied by metal accounts for around 45.5% of the total cross-section. Wire ropes with the construction 6 x 37 + 1 FC are also favored. These have the same fill factor.
 |
Determining the diameter of a steel wire rope: 16 mm |
Using a rule of thumb, the breaking load and MSL of single-use wire ropes can be calculated as follows:
| Breaking load | MSL factor | MSL | |
| 1.6 x 1.6 x 50 = 128 kN | x 0.80 = | 102.4 kN | (diameter in cm) |
| 16 x 16 x 50 = 12,800 daN | x 0.80 = | 10,240 daN | (diameter in mm) |
Since the of 80% of 50 equates to a value of 40, the MSL can also be calculated directly with an easily remembered formula:
| MSL single-use steel wire ropes of the above type = d x d x 40 |
It would be a little quicker to calculate the MSL using the direct rule of thumb:
| MSL for steel wire rope, 1.6 cm thick = 1.6 x 1.6 x 40 = 102.4 kN |
| MSL for steel wire, 16 mm thick = 16 x 16 x 40 = 10,240 daN |
 |
Use of a 16 mm-thick steel wire rope on a platform container |
Using steel ropes of this kind is a waste of materials, since the high MSL value is out of proportion to that of the lashing points on the containers. The strongest lashing rings have an MSL value of 8,000 daN, many are around 5,000 daN and most are around 3,000 - 4,000 daN. To for homogeneous lashings, it is usually perfectly sufficient to use wire ropes of a smaller diameter. For instance, 12 mm wires:
| MSL for steel wire rope, 1.2 cm thick = 1.2 x 1.2 x 40 = 5.76 kN |
| MSL for steel wire, 12 mm thick = 12 x 12 x 40 = 5,760 daN |
Different MSL values must be applied for reusable wire ropes. Wires of this kind must only be calculated with 30% of the breaking load for the MSL:
| Breaking load | MSL factor | MSL | |
| 1.6 x 1.6 x 50 = 128 kN | x 0.30 = | 38.4 kN | (diameter in cm) |
| 16 x 16 x 50 = 12,800 daN | x 0.30 = | 3,840 daN | (diameter in mm) |
 |
 |
|
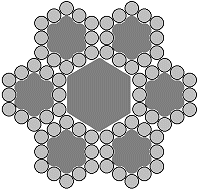
| 6 x 12 +7 FC | 6 x 18 +7 FC |
Significantly lower fill factors are exhibited by wire ropes with constructions such as 6 x 9 + 7 FC, 6 x 12 + 7 FC, 6 x 15 + 7 FC, 6 x 18 + 7 FC or similar, where, as the designation already indicates, a fiber filler has been incorporated in the center of each strand. Ropes of this kind are frequently used by Dutch and Belgian companies as lashing wires.
The breaking loads and MSLs of wires of this kind are only half as high, because a factor of 25 rather than a factor of 50 has to be used for calculation.
| Breaking load | MSL factor | MSL | |
| d x d x 25 | x 0.80 = | kN | (diameter in cm) |
| d x d x 25 | x 0.80 = | daN | (diameter in mm) |
The same applies for re-usable wire ropes of this type:
| Breaking load | MSL factor | MSL | |
| d x d x 25 | x 0.30 = | kN | (diameter in cm) |
| d x d x 25 | x 0.30 = | daN | (diameter in mm) |
 |
Steel wire rope coil |
When ordering wire ropes, the following details should be stipulated to ensure that the correct rope type will be received:
| - | Diameter in mm or inches | e.g. 16 mm or 5/8" |
| - | Quantity and length | e.g. 20 x 200 m |
| - | Rope construction | e.g. 6 x 19 + 1 FE |
| - | Type and direction of lay | e.g. cross lay, to the right |
| - | Special features (plain, galvanized etc.) | e.g. plain |
| - | Nominal strength | e.g. 1570 N/mm² |
| - | Greasing | e.g. normal |
| - | Termination: swaged / sharpened | e.g. swaged |
| - | Packaging | e.g. coils |
 |
 |
||
| Cutting wire ropes with shears | |||
| Incorrect - small lever arm |
Correct - large lever arm |
||
Wire ropes can be cut to length with hydraulic shears or other special tools if larger quantities need to be processed. Handshears are sufficient on site and with small quantities.
 |
Wires can be damaged by sharp edges. |
Running wires around sharp edges will lower their MSL. There are precise values, but a number of additional factors should be taken into account. Rough but nonetheless usable values are provided in this easily remembered table:
 |
|
| MSL of a single run at various bending angles |
You will find an example showing exact values in Volume II.
 |
 |
Wire ropes with spliced or pressed eyes are rarely used for lashing. Generally, wire cable clamps (clips) are used to connect to other lashing elements, such as turnbuckles, shackles, lashing rings etc. There are suitable clips available for every thickness of rope, in both metric and Imperial sizes. For a 12 mm wire, 12 mm or ½" clips are required. For 16 mm wires, 16 mm or 5/8" clips must be provided.
When the nuts are correctly tightened as described further below, the following figures can be seen as guideline values for the strength of wire cable clips with common rope diameters.
 |
At a sufficient tightening torque: 1 clip = 25% MSL |
Up to 25% of the MSL can be achieved with one clip. If - as in this case - there is no tightening torque, the value approaches 0.
 |
|
| At a sufficient tightening torque: 2 clips = 50% MSL |
50% of the MSL of the wire rope is achieved using two wire cable clips. The indentations in the wire indicate a good tightening torque. The following rule of thumb applies: if the free end on which the U-bolts of the wire cable clips should be placed is crushed to half the thickness of the wire, the clips have been tightened to a sufficient torque.
 |
Only with a sufficient tightening torque and correctly attached clips: 3 clips = 75% MSL |
The wire cable clips have been attached incorrectly and the tightening torques are too low. The MSL of lashings of this kind is usually overestimated. An maximum MSL of approximately 75% can be achieved with three wire cable clips.
 |
 |
|
| Incorrectly attached wire cable clips in insufficient quantity |
All too often in practice, too few wire cable clips are used or they are attached incorrectly. Often, the nuts are not tightened sufficiently. The wires slip through the wire cable clips under load.
 |
Wires which have slipped through where only two wire cable clips were attached |
If a wire rope lashing is to be homogeneous, four wire cable clips must be placed with the U-bolt on the free end.:
 |
|
| Single cable with eye |
This type of attachment is advisable if relatively long lashings have to be made. They are usually not necessary for container loads.
| Sling or double run - unsuitable construction |
This construction is often used for shorter lashings. But it should not be made like this.
 |
|
| Sling or double run - ideal construction |
This format should always be used for relatively short lashings because it is the most resilient. Inadequacies such as the presence of sharp edges can also be counteracted with this method.
Where possible, work should be carried out as demonstrated here.
 |
|
| Positive example - wire rope arranged correctly, wire cable clips attached correctly and sufficiently high tightening torque on the nuts |
 |
Lashing is a technically demanding task which has to be learnt. Otherwise, errors creep in even with the best will in the world. | |
| Lashing which is not homogeneous |
 |
 |
|
| Anchor shackle | Chain shackle |
Anchor shackles should be preferred for use as lashing shackles. They can adapt better to the directions in which forces arise.
Using a rule of thumb, the breaking load and MSL of lashing shackles can be calculated as follows:
| Breaking load | MSL factor | MSL | |
| d x d x 20 | x 0.50 = | kN | (diameter in cm) |
| d x d x 20 | x 0.50 = | daN | (diameter in mm) |
Since the factor 50% of 20 is equivalent to 10, the MSL can also be calculated directly with an easy-to-remember formula:
| MSL for lashing shackle = d x d x 10 |
 |
Determining the diameter of a bolt on a lashing shackle: 26 mm |
The diameter of the bolt is first measured in centimeters or millimeters. The breaking load formula only applies to shackles made of standard strength steel. The value for this shackle is quickly calculated using the direct rule of thumb for the MSL.
| MSL for lashing shackle bolt of diameter 2.6 cm = 2.6 x 2.6 x 10 = 67.6 kN |
| MSL for lashing shackle bolt of diameter 26 mm = 26 x 26 x 10 = 6,760 daN |
 |
|
| Lashing turnbuckle with very well worked weld seams |
The same values apply to turnbuckles as to lashing shackles. The diameter of the thread is first measured in centimeters or millimeters. The breaking load formula only applies to turnbuckles made of standard strength steel. The value for this turnbuckle is quickly calculated using the direct rule of thumb for the MSL, if the thread was measured at 1 1/8 inch = 28.575 mm.
| MSL for lashing turnbuckle of thread diameter 2.86 cm = 2.86 x 2.86 x 10 = 81.796 kN |
| MSL for lashing turnbuckle of thread diameter 28.6 mm = 2.86 x 2.86 x 10 = 8,179.6 daN |
When purchasing turnbuckles, it is important that only turnbuckles with sufficiently wide nuts and weld seams are purchased. Spot welded turnbuckles are available on the market. These should not be used.
The turnbuckle shown above is generally available in three sizes: 1 1/8 " , 1¼" and 1½" thread diameter. 1 inch is equivalent to 25.4 mm.
 |
Turnbuckle made of higher strength steel for round steel chains with short links |
The manufacturer's specifications must be observed for turnbuckles made of higher strength steel. 50% of the specified breaking load is assumed as the MSL. Unless, as with this turnbuckle, a WLL (Working Load Limit) has already been specified. This then corresponds to the MSL.
 |
|
| Tag on a lashing turnbuckle |