Container Handbook: 4.2 Prevailing load case

4.2 Prevailing load case

In the applicable load case the beam rests on the internal bottom of the container with its entire length t and carries a symmetrical homogeneous load m over the length r (Figure 15). Under the assumption of a homogeneous load distribution from below and from the top the beam is subject to a bending moment of the magnitude:

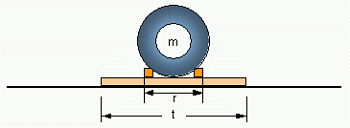
Figure 15: Beam with linear load and linear support

The required section modulus results

for timber beams: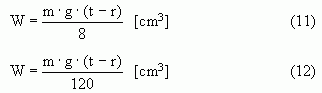
for steel beams:

In this load case the effective length t must be limited against r, because a too long beam would lift its ends off the ground and would no longer transfer the load fairly evenly to the ground. For this limitation the following rules of thumb are given:

Timber beams 10 x 10 cm:   t_max = (1.2 · r + 0.8) m, but not more than (r + 1.0) m

Timber beams 15 x 15 cm:   t_max = (1.2 · r + 1.5) m, but not more than (r + 2.0) m

Timber beams 20 x 20 cm:   t_max = (1.2 · r + 2.0) m, but not more than (r + 3.0) m

Steel beams 12 x 12 cm:   t_max = (1.2 · r + 3.0) m, but not more than (r + 4.0) m

Steel beams 14 x 14 cm:   t_max = (1.2 · r + 3.2) m, but not more than (r + 4.2) m

Steel beams 16 x 16 cm:   t_max = (1.2 · r + 3.4) m, but not more than (r + 4.4) m

Steel beams 18 x 18 cm:   t_max = (1.2 · r + 3.6) m, but not more than (r + 4.6) m