Es wird aber deutlich, dass für Coils der Gewichtsklasse XH, bei denen die Balkenlänge t nach Bild 13 größer als 2.7 m und damit der Balkenüberstand größer als 1.5 m zu erwarten ist, eine korrekte Lastverteilung mit Holzbalken nicht mehr mit vertretbarem Aufwand zu erreichen ist. Deshalb werden in Bild 17 in einem vergleichbaren Diagramm die Lösungen der Gleichung (12) für Stahlträger dargestellt.
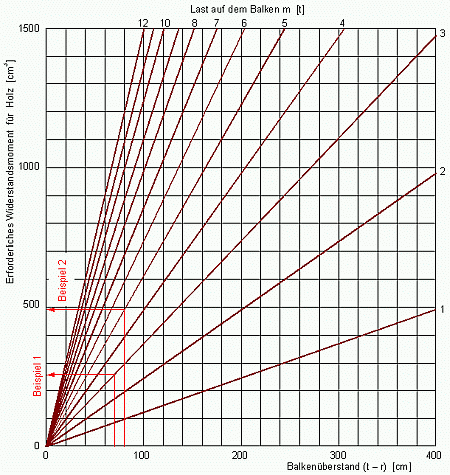
Bild 16: Erforderliches Widerstandsmoment für untergelegte Holzbalken
Beispiel 1: Ein Coil von 6 t Masse auf Skids von 0.9 m Balkenlänge wird auf zwei Längsbalken von 1.6 m Länge gelegt. Der Balkenüberstand (t - r) beträgt 70 cm. Jeder Balken wird mit 3 t belastet. Das Diagramm in Bild 16 ergibt ein erforderliches Widerstandsmoment von ca. 260 cm³. Damit sind Balken von 12 x 12 cm Querschnitt erforderlich (Tabelle 1).
Beispiel 2: Ein Coil von 10 t Masse auf Skids von 1.0 m Balkenlänge wird auf zwei Längsbalken von 1.8 m Länge gelegt. Der Balkenüberstand (t - r) beträgt 80 cm. Jeder Balken wird mit 5 t belastet. Das Diagramm in Bild 16 ergibt ein erforderliches Widerstandsmoment von ca. 490 cm³. Damit sind Balken von 15 x 15 cm Querschnitt gerade ausreichend (Tabelle 1).
Beispiel 3: Ein Coil von 21 t Masse und mC/P = 0.75 benötigt nach Bild 13 zur Sicherung der Längsfestigkeit des Containers zwei Träger von 3.9 m Länge. Die Einzellast von 10.5 t wird auf jeden Träger über eine Länge von ca. 1.3 m übertragen. Damit beträgt der Balkenüberstand (t - r) rund 260 cm. Das Diagramm in Bild 17 ergibt mit diesem Eingang ein erforderliches Widerstandsmoment von ca. 225 cm³. Damit sind Träger von 14 x 14 cm gerade nicht mehr ausreichend (Tabelle 2). Es sollten stärkere verwendet werden.
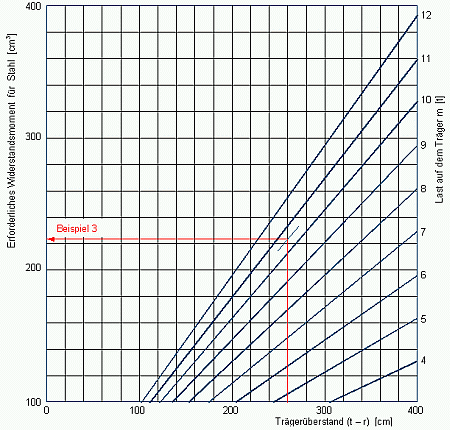
Bild 17: Erforderliches Widerstandsmoment für untergelegte Stahlträger